Gradient descent is a spectacularly effective optimization technique, but it's not the only method for optimizing non-convex functions. There are a number of alternative numerical methods that can be used to solve functions without using or calculating the gradient of that function (or indeed, where the gradient of such function isn't known).
The Nelder-Mead algorithm is one such numerical method that was first proposed in 1965. As we'll see, the method is actually quite straightforward, evaluating the function at various points within a neighbourhood, then iteratively moving those points in the optimal direction until convergence.
Assume we have some task T, like constraint solving, image classification. For current purposes, it doesn't really matter what this task is. We just know that our task takes some input $x$, and we want to solve it by producing some numerical output.
To do this, we formulate the task as some function $f$ of $x$ and parameters $\theta$.
With this formulation, the minimum of the function (i.e. $\min f(x;\theta)$) is the optimal solution for T.
Let's leave aside how we decided this formulation (or the parameterization of that function). That's obviously a critical step in the optimization process, just not the focus of this post.
So we want to minimize $f(x;\theta)$ to find the best parameters for our task T.
The logic behind NM is quite straightforward - evaluate the objective function at a few random points, try and move the worst point towards the middle of the first two, and repeat until the points converge to the minimum.
Let's look at a function where we know the minimum, like $f(x) = x^2$. We'll work in two dimensions to make things easier to visualize.
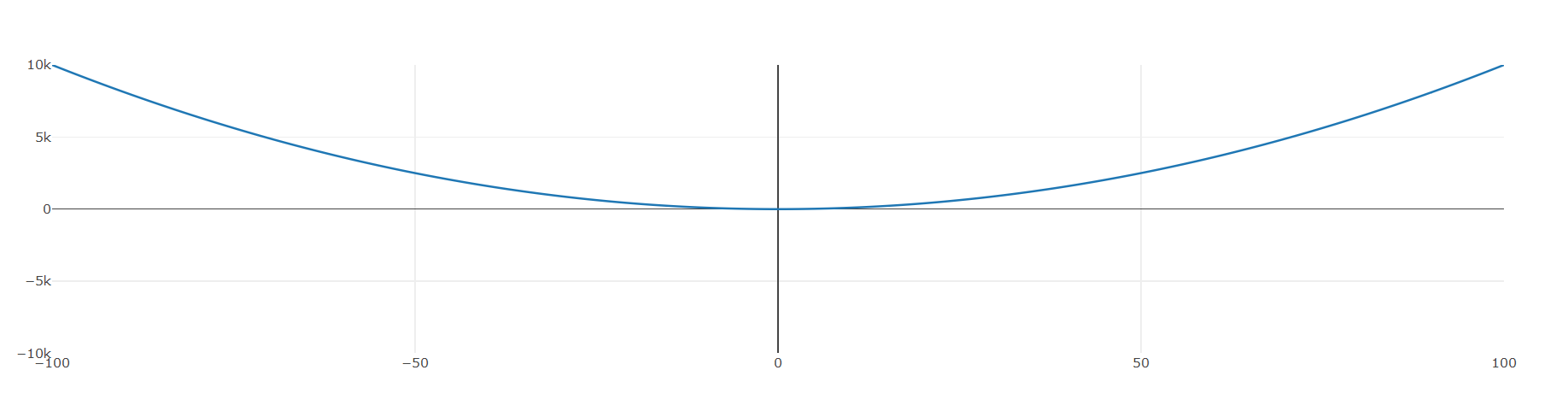
NM starts a set of n+1 random points (where n is the dimensionality of the domain of $f$). This is known as a simplex, and in two dimensions, forms a triangle. Our input here is only one-dimensional, so the simplex is simply a line-segment - but I chose three points anyway for the purpose of illustration.
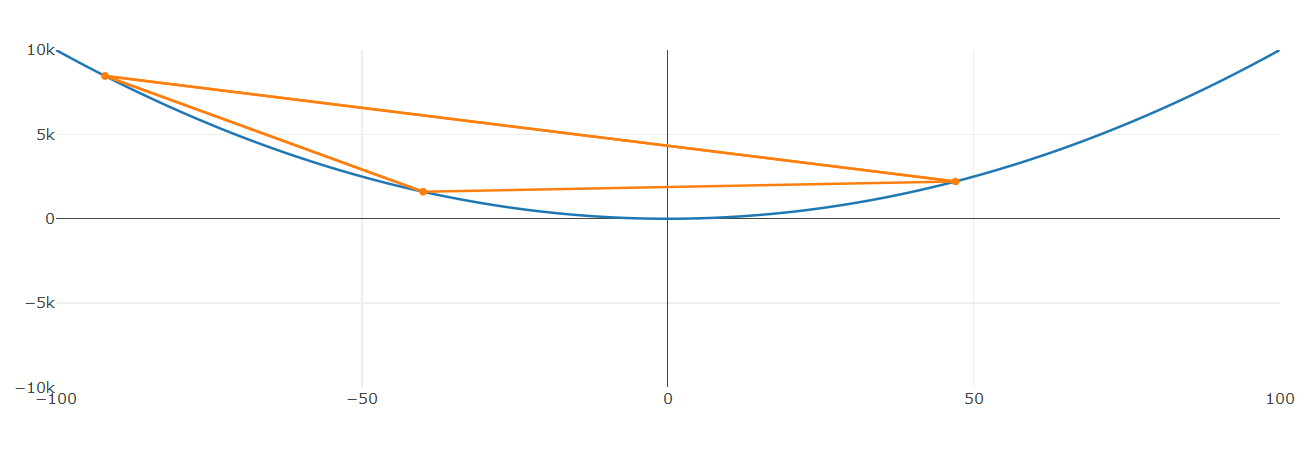
These points are then sorted according to their performance under their objective function - leaving us with points B, G and W (think "best", "good", and "worst").
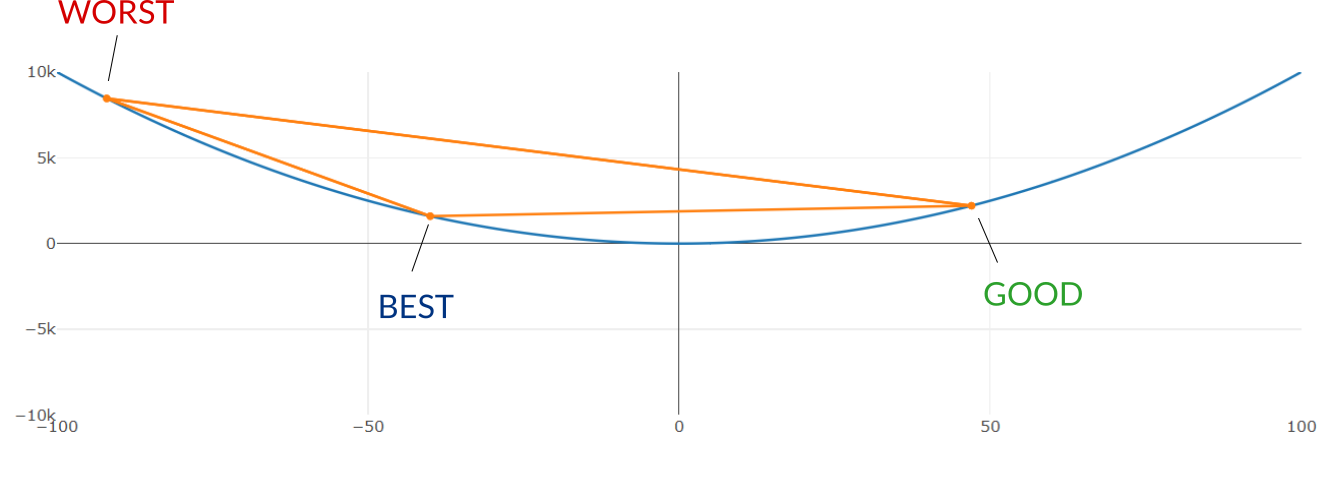
NM then finds the midpoint M between B and G, and performs a sequence of different transformations to M, evaluating the objective function at M and comparing it with the function evaluated at B or G.
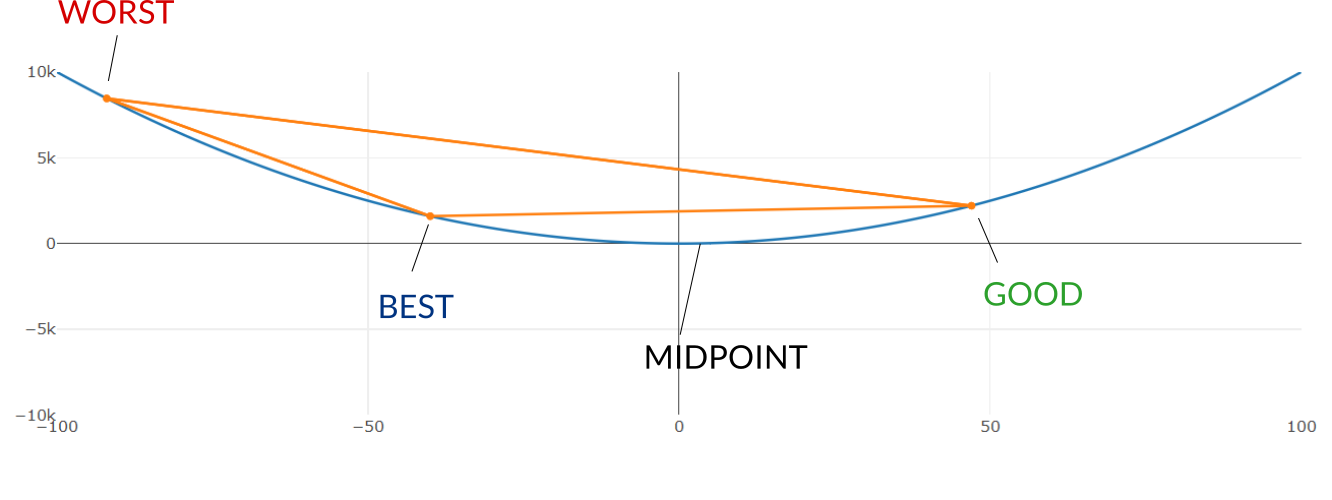
For example, M is first reflected towards W - if this reflection R performs better than B (i.e. the objective function evaluated at R is closer to zero than evaluated at B), an extension is performed in the same direction.

Depending on which is better, point W is replaced with point R. Alternatively, if the reflection performs worse, the midpoint is contracted or shrunk in the same direction as W.

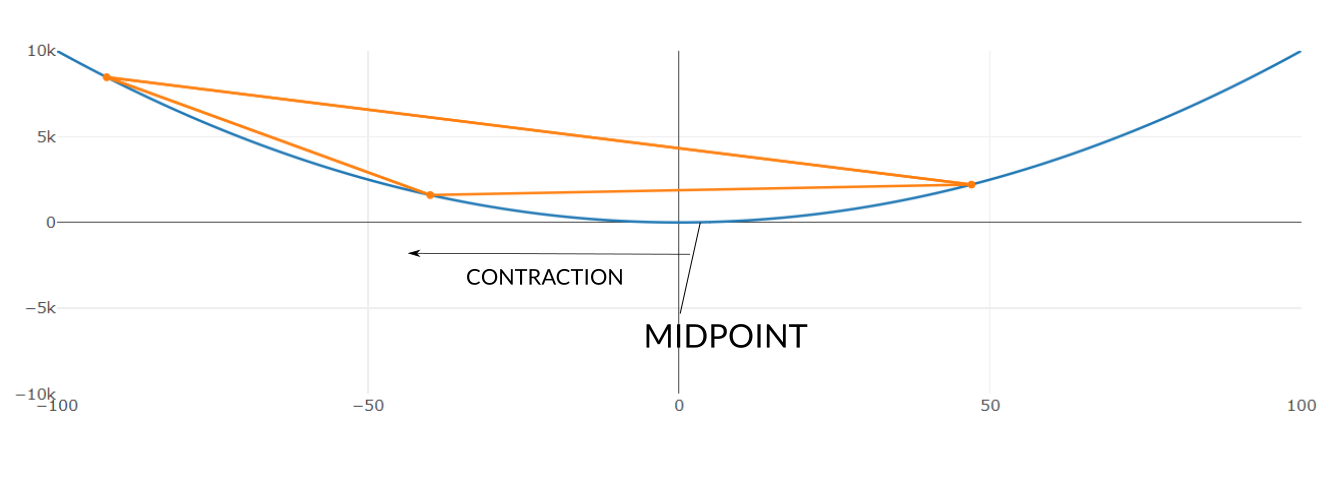
This process is repeated until the distance between the original and transformed points falls beneath some threshold.
Here is an F# implementation for Nelder Mead:
{{< highlight fsharp >}} type Simplex(points:Point[], objective:Point -> float) =
let scored = points
|> Array.map( fun x -> x, objective x)
|> Array.sortBy (fun (x,y) -> y)
let best = fst scored.[0]
let f_best = snd scored.[0]
let good = fst scored.[1]
let f_good = snd scored.[1]
let worst = fst scored.[2]
let f_worst = snd scored.[2]
let midpoint = (best + good) / 2.0
member this.compute () =
let reflect = (midpoint * 2.0) - worst
let f_reflect = objective reflect
match f_reflect < f_good with
| true ->
match f_best < f_reflect with
| true ->
Simplex([|best; good; reflect|], objective)
| false ->
let extension = (reflect * 2) - midpoint
let f_extension = objective extension
match f_extension < f_reflect with
| true ->
Simplex([|best; good; extension|], objective)
| false ->
Simplex([|best; good; reflect|], objective)
| false ->
match f_reflect < f_worst with
| true ->
Simplex([|best; good; reflect|], objective)
| false ->
let c1 = (midpoint + worst) / 2
let c2 = (midpoint + reflect) / 2
let contraction = match objective c1 > objective c2 with | true -> c2 | false -> c1
let f_contraction = objective contraction
match f_contraction < f_worst with
| true ->
Simplex([|best; good; contraction|], objective)
| false ->
let shrinkage = (best + worst) / 2
let f_shrinkage = objective shrinkage
Simplex([|best; midpoint; shrinkage|], objective)
{{< / highlight >}}
This is a fairly bare-bones implementation (the canonical version should contain scale parameters for each transformation and checks at each iteration to ensure the simplex has actually shrunk).
This was also a good opportunity to take Fable for a spin. Fable is a transpiler, letting you write F# code that will run/render in the browser. Here's Nelder-Mead in action, running courtesy of Fable.
Click "Reset" to reset the simplex to three randomly chosen points, then click "Step" to go through one iteration of Nelder-Mead. You'll see the simplex converging to 0 - the optimal solution for our basic function.
One of the cool things about this is that the above uses Plotly.js for charting library, all invoked from F# code. ts2fable is a Typescript to F# transpiler bundled with , letting you generate F# bindings for any Typescript library. This allowed me to take the Plotly.js definitions from the DefinitelyTyped project, generate F# bindings and stitch the Nelder-Mead algorithm/buttons to the chart, all via F#. Nifty, right?
Admittedly, the project is still relatively young so it's not all smooth sailing (and ts2fable in particular generates some odd code that needed manual fixing).
But seeing the F# language venture beyond the .NET runtime is very promising. I initially tried a Javascript implementation of Nelder-Mead. Not only was it literally twice as long as the F# version, and only half as comprehensible. I find ML-style pattern matching an excellent idiom for representing algorithmic work concisely and with minimal clutter.
Code is available on GitHub if you want to check it out.
Header image courtesy of Flickr